Abstract

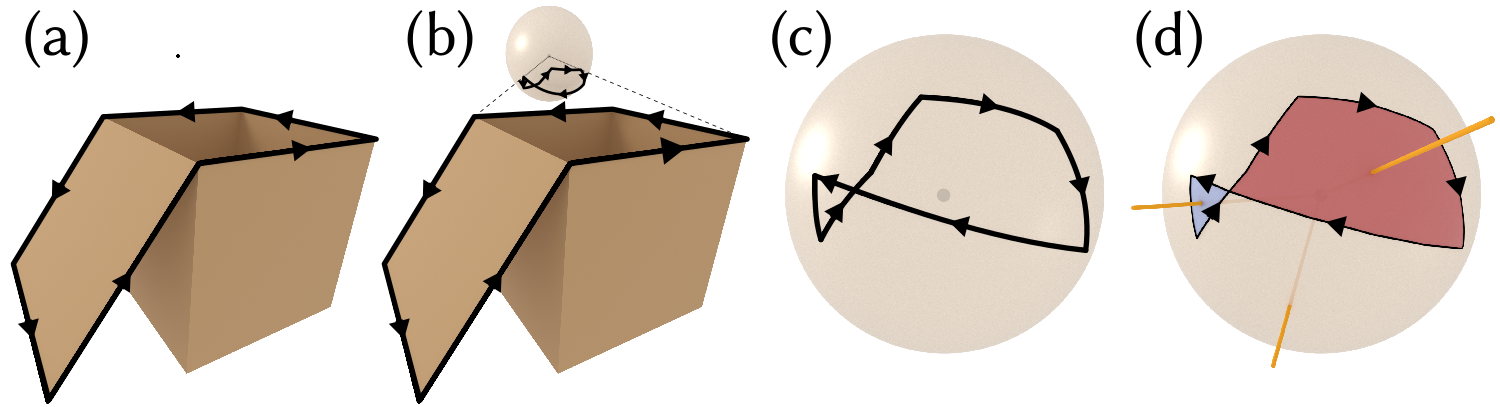
The generalized winding number is an essential part of the geometry processing toolkit, allowing to quantify how much a given point is inside a surface, even when the surface has boundaries and noise. We propose a new universal method to compute a generalized winding number, based only on the surface boundary and the intersections of a single ray with the surface, supporting any oriented surface representations that support a ray intersection query. Due to the focus on the boundary, our algorithm has a unique set of properties. For 2D parametric curves, on a regular grid of query points, our method is up to 4× faster than the current state of the art, maintaining the same precision. In 3D, our method can compute a winding number of a surface without discretizing it, including parametric surfaces. For some meshes with many triangles and a simple boundary, our method is faster than the hierarchical evaluation of the generalized winding number while still being precise. Similarly, on some parametric surfaces with a simple boundary, our method can be faster than adaptive quadrature. We validate our algorithms theoretically, numerically, and by demonstrating a gallery of results on a variety of parametric surfaces and meshes, as well uses in a variety of applications, including voxelizations and boolean operations.